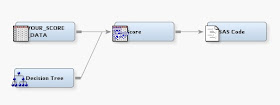
The following diagram indicates the schema for scoring data in SAS Enterprise Miner. The SAS Code node is necessary for telling Enterprise Miner where the data to be scored is located, and where the model information is that will be used for scoring.
/* CODE TO BE ENTERED IN THE SAS CODE NODE */
/* THE SCORE DATA MUST BE IN A LIBRARY */
/* ACCESSIBLE TO ENTERPRISE MINER */
DATA YOUR_LIBRARY.YOUR_SCORE_DATA;
SET &EM_IMPORT_SCORE;
RUN;
/* THE CODE IN THE SET STATEMENT IS GENERIC CODE THAT SEEMS TO WORK
ANY WHERE IN THE PROJECT AS LONG AS IT FOLLOWS THE 'SCORE' NODE*/
An attempt to make sense of econometrics, biostatistics, machine learning, experimental design, bioinformatics, ....
Tuesday, February 22, 2011
Tuesday, February 15, 2011
Tuesday, February 1, 2011
Interaction Models
Given a model of the form:
y= β0 + β1 X+ β2Z + β3 XZ+ e
the relationship between X and Y is conditional on Z. The interaction term represents the effect of X on Y conditional on the value of Z.
In ‘Understanding Interaction Models: Improving Empirical Analysis’ by Brambor, Clark, and Golder the following schematic is presented:
As the schematic shows, β2 represents the difference in intercepts between the two regression lines.
Notes:
Marginal Effect of X on Y: ∂Y/ ∂X = β1 + β3 Z
β1 = effect of X on Y when Z =0
If XY is significant, that implies that the relationship between X and Y differs significantly between classes or values of Z.
It is possible that the effect of X on Y is significant for some values of Z even if the interaction term is not, hence you cannot base the inclusion of XZ in the model on the significance of the interaction term (Bramber et al, 2005).
In determining significance, the basic regression output typically does not provide sufficient information and modifications are required (Bramber et al, 2005).
Kmenta (1971) provides the following comments regarding the significance of interactions and constitutive terms:
“When there are interaction terms in the equation, then any given explanatory variable may be represented not by one but several regressors. The hypothesis that this variable does not influence Y means that the coefficients of all regressors involving this variable are jointly zero”
As a result, the significance of X and the XZ term is given by the following F-test:
F = [ (R22 – R21) / (k2 – k1 )] / [(1-R22) / (N- k2 -1)
Kn = # of variables in each model respectively (model including and excluding the interaction term and interaction variable)
R2n = R-square for each respective model
N = total observations
The standard error of β1 + β3 Z = sqrt(V(β1) + Z2 V(β3 ) + 2 Z COV(β1 ,β3))
Constructing Odds Ratios from Logistic Models: e β1 + β3 Z
References:
Understanding Interaction Models: Improving Empirical Analyses. Thomas Bramber, William Roberts Clark, Matt Golder. Political Analysis (2006) 14:63-82
Elements of Econometrics. Jan Kmenta. Macmillan (1971)