Data Mining in A Nutshell

# The following code may look rough, but simply paste into R or

# a text editor (especially Notepad++) and it will look

# much better.

# PROGRAM NAME: MACHINE_LEARNING_R

# DATE: 4/19/2010

# AUTHOR : MATT BOGARD

# PURPOSE: BASIC EXAMPLES OF MACHINE LEARNING IMPLEMENTATIONS IN R

# DATA USED: GENERATED VIA SIMULATION IN PROGRAM

# COMMENTS: CODE ADAPTED FROM : Joshua Reich (josh@i2pi.com) April 2, 2009

# SUPPORT VECTOR MACHINE CODE ALSO BASED ON :

# ëSupport Vector Machines in Rî Journal of Statistical Software April 2006 Vol 15 Issue 9

#

# CONTENTS: SUPPORT VECTOR MACHINES

# DECISION TREES

# NEURAL NETWORK

# load packages

library(rpart)
library(MASS)
library(class)
library(e1071)

# get data

# A simple function for producing n random samples

# from a multivariate normal distribution with mean mu

# and covariance matrix sigma

rmulnorm <- function (n, mu, sigma) {

    M <- t(chol(sigma))
    d <- nrow(sigma)
    Z <- matrix(rnorm(d*n),d,n)
    t(M %*% Z + mu)
}

# Produce a confusion matrix

# there is a potential bug in here if columns are tied for ordering

cm <- function (actual, predicted)

{
   
    t<-table(predicted,actual) 
    t[apply(t,2,function(c) order(-c)[1]),]
}

# Total number of observations

N <- 1000 * 3

# Number of training observations

Ntrain <- N * 0.7

# The data that we will be using for the demonstration consists

# of a mixture of 3 multivariate normal distributions. The goal

# is to come up with a classification system that can tell us,

# given a pair of coordinates, from which distribution the data

# arises.

A <- rmulnorm (N/3, c(1,1), matrix(c(4,-6,-6,18), 2,2))
B <- rmulnorm (N/3, c(8,1), matrix(c(1,0,0,1), 2,2))
C <- rmulnorm (N/3, c(3,8), matrix(c(4,0.5,0.5,2), 2,2))

data <- data.frame(rbind (A,B,C))
colnames(data) <- c('x', 'y')
data$class <- c(rep('A', N/3), rep('B', N/3), rep('C', N/3))

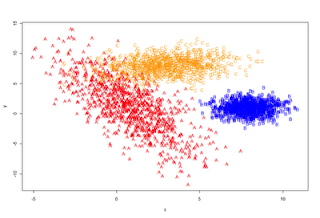
# Lets have a look

plot_it <- function () {
    plot (data[,1:2], type='n')
    points(A, pch='A', col='red')
    points(B, pch='B', col='blue')
    points(C, pch='C', col='orange')
}
plot_it()

# Randomly arrange the data and divide it into a training

# and test set.

data <- data[sample(1:N),]
train <- data[1:Ntrain,]
test <- data[(Ntrain+1):N,]

# SVM

# Support vector machines take the next step from LDA/QDA. However

# instead of making linear voronoi boundaries between the cluster

# means, we concern ourselves primarily with the points on the

# boundaries between the clusters. These boundary points define

# the 'support vector'. Between two completely separable clusters

# there are two support vectors and a margin of empty space

# between them. The SVM optimization technique seeks to maximize

# the margin by choosing a hyperplane between the support vectors

# of the opposing clusters. For non-separable clusters, a slack

# constraint is added to allow for a small number of points to

# lie inside the margin space. The Cost parameter defines how

# to choose the optimal classifier given the presence of points

# inside the margin. Using the kernel trick (see Mercer's theorem)

# we can get around the requirement for linear separation

# by representing the mapping from the linear feature space to

# some other non-linear space that maximizes separation. Normally

# a kernel would be used to define this mapping, but with the

# kernel trick, we can represent this kernel as a dot product.

# In the end, we don't even have to define the transform between

# spaces, only the dot product distance metric. This leaves

# this algorithm much the same, but with the addition of

# parameters that define this metric. The default kernel used

# is a radial kernel, similar to the kernel defined in my

# kernel method example. The addition is a term, gamma, to

# add a regularization term to weight the importance of distance.

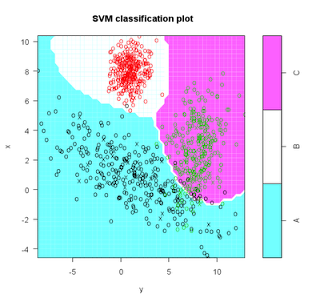
s <- svm( I(factor(class)) ~ x + y, data = train, cost = 100, gama = 1)

s # print model results

#plot model and classification-my code not originally part of this

plot(s,test)

(m <- cm(train$class, predict(s)))
1 - sum(diag(m)) / sum(m)

(m <- cm(test$class, predict(s, test[,1:2])))
1 - sum(diag(m)) / sum(m)

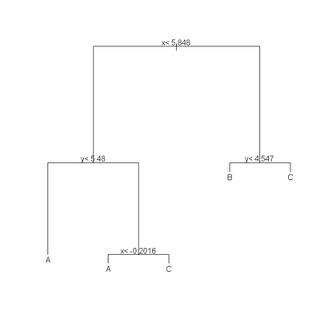
# Recursive Partitioning / Regression Trees

# rpart() implements an algorithm that attempts to recursively split

# the data such that each split best partitions the space according

# to the classification. In a simple one-dimensional case with binary

# classification, the first split will occur at the point on the line

# where there is the biggest difference between the proportion of

# cases on either side of that point. The algorithm continues to

# split the space until a stopping condition is reached. Once the

# tree of splits is produced it can be pruned using regularization

# parameters that seek to ameliorate overfitting.

names(train)
names(test)

(r <- rpart(class ~ x + y, data = train)) plot(r) text(r) summary(r) plotcp(r) printcp(r) rsq.rpart(r)

cat("\nTEST DATA Error Matrix - Counts\n\n")
print(table(predict(r, test, type="class"),test$class, dnn=c("Predicted", "Actual")))

# Here we look at the confusion matrix and overall error rate from applying

# the tree rules to the training data.

predicted <- as.numeric(apply(predict(r), 1, function(r) order(-r)[1]))
(m <- cm (train$class, predicted))
1 - sum(diag(m)) / sum(m)


# Neural Network

# Recall from the heuristic on data mining and machine learning , a neural network is # a nonlinear model of complex relationships composed of multiple 'hidden' layers

# (similar to composite functions)

# Build the NNet model.

require(nnet, quietly=TRUE)

crs_nnet <- nnet(as.factor(class) ~ ., data=train, size=10, skip=TRUE, trace=FALSE, maxit=1000)

# Print the results of the modelling.

print(crs_nnet)
print("

Network Weights:

")
print(summary(crs_nnet))

# Evaluate Model Performance

# Generate an Error Matrix for the Neural Net model.

# Obtain the response from the Neural Net model.

crs_pr <- predict(crs_nnet, train, type="class")

# Now generate the error matrix.

table(crs_pr, train$class, dnn=c("Predicted", "Actual"))

# Generate error matrix showing percentages.

round(100*table(crs_pr, train$class, dnn=c("Predicted", "Actual"))/length(crs_pr))

Calucate overall error percentage.

print( "Overall Error Rate")

(function(x){ if (nrow(x) == 2) cat((x[1,2]+x[2,1])/sum(x)) else cat(1-(x[1,rownames(x)])/sum(x))}) (table(crs_pr, train$class, dnn=c("Predicted", "Actual")))