Y = f(g(h(x)) or
x -> hidden layers ->Y
Example 1 With a logistic/sigmoidal activation function, a neural network can be visualized as a sum of weighted logits:
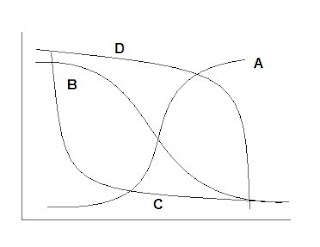
Y = α Σ wi e θi/1 + e θi + ε
wi = weights θ = linear function Xβ
Y= 2 + w1 Logit A + w2 Logit B + w3 Logit C + w4 Logit D
( Adapted from ‘A Guide to Econometrics, Kennedy, 2003)
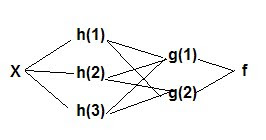
Example 2
Where: Y= W0 + W1 Logit H1 + W2 Logit H2 + W3 Logit H3 + W4 Logit H4 and
H1= logit(w10 +w11 x1 + w12 x2 )
H2 = logit(w20 +w21 x1 + w22 x2 )
H3 = logit(w30 +w31 x1 + w32 x2 )
The links between each layer in the diagram correspond to the weights (w’s) in each equation. The weights can be estimated via back propagation.
( Adapted from ‘A Guide to Econometrics, Kennedy, 2003 and Applied Analytics Using SAS Enterprise Miner 6.1)
MULTILAYER PERCEPTRON: a neural network architecture that has one or more hidden layers, specifically having linear combination functions in the hidden and output layers, and sigmoidal activation functions in the hidden layers. (note: a basic logistic regression function can be visualized as a single layer perceptron)
RADIAL BASIS FUNCTION (architecture): a neural network architecture with exponential or softmax (generalized multinomial logistic) activation functions and radial basis combination functions in the hidden layers and linear combination functions in the output layers.
RADIAL BASIS FUNCTION: A combination function that is based on the Euclidean distance between inputs and weights
ACTIVATION FUNCTION: formula used for transforming values from inputs and the outputs in a neural network.
COMBINATION FUNCTION: formula used for combining transformed values from activation functions in neural networks.
HIDDEN LAYER: The layer between input and output layers in a neural network.
HIDDEN LAYER: The layer between input and output layers in a neural network.


No comments:
Post a Comment