Remarks from Literature:
‘The basic idea of Bayesian Model Averaging (BMA) is to make inferences based on a weighted average over model space.’ (Hoeting*)
‘BMA accounts for uncertainty in (an) estimated logistic regression by taking a weighted average of the maximum likelihood estimates produced by our models…and may be superior to stepwise regression’ ( Goenner and Pauls, 2006)
‘The uniform prior ( which assumes that each of the K models is equally likely)… is typical in cases that lack strong prior beliefs.’ (Goenner and Pauls, 2006 and Raftery 1995).
References:
Goenner , Cullen F. and Kenton Pauls. ‘A Predictive Model of Inquiry to Enrollment.’ Research in Higher Education, Vol 47, No 8, December 2006.
*Jennifer A. Hoeting, Colorado State Univeristy. ‘Methodology for Bayesian Model Averaging: An Update’
Hoeting, Madigan, Reftery, and Volinksy. ‘ Bayesian Model Averaging: A Tutorial.’ Statistical Science 1999, Vol 14, No 4, 382-417.
Peter Kennedy. ‘A Guide to Econometrics.’ 5th Edition. 2003 MIT Press
Raftery, Madian and Hoeting. ‘Bayesian Model Averaging for Linear Regression Models.’ Journal of the American Statistical Association (1997) 92, 179-191
Raftery A.E. ‘Bayesian Model Selection in Social Research .’ In: Marsden, P.V. (ed): Sociological Methodology 1995, Blackwells Publishers, Cambridge, MA, pp. 111-163.
Studenmund, A.H. Using Econometrics A Practical Guide. 4th Ed. Addison Wesley. 2001
SAS/STAT 9.2 User’s Guide. Introduction to Bayesian Analysis Procedures.
An attempt to make sense of econometrics, biostatistics, machine learning, experimental design, bioinformatics, ....
Wednesday, September 22, 2010
Tuesday, September 21, 2010
Path Analysis
Partial Least Squares
Monday, September 20, 2010
Why study Applied/Agricultural Economics?
Why study Applied/Agricultural Economics? (for an updated post on this topic see here.)
"The combination of quantitative training and applied work makes agricultural economics graduates an extremely well-prepared source of employees for private industry. That's why American Express has hired over 80 agricultural economists since 1990." - David Edwards, Vice President-International Risk Management, American Express
Applied Economics is a broad field covering many topics beyond those stereotypically thought of as pertaining to agriculture. These may include finance and risk management, environmental and natural resource economics, behavioral economics, game theory, or public policy analysis to name a few. More and more 'Agricultural Economics' is becoming synonymous with 'Applied Economics.' Many departments have changed their name from Agricultural Economics to Agricultural and Applied Economics and some have even changed their degree program names to just 'Applied Economics.' In 2008, the American Agricultural Economics Association changed its name to the Agricultural and Applied Economics Association.
This trend is noted in recent research in the journal Applied Economic Perspectives and Policy:
"Increased work in areas such as agribusiness, rural development, and environmental economics is making it more difficult to maintain one umbrella organization or to use the title “agricultural economist” ... the number of departments named" Agricultural Economics” has fallen from 36 in 1956 to 9 in 2007."
Agricultural/Applied economics provides students with skills in high demand, particularly in the area of analytics.
"Some companies have built their very business on their ability to collect, analyze, and act on data." (See 'Competing on Analytics." Harvard Bus.Review Jan 2006)
In a recent blog post, SAS (a leader in applied analytics, big data, and software solutions) highlights the fact that they find people with applied economics backgrounds among their exectives:
"computer science may not be the best place to find data scientists....Over the years many of our senior executives have had degrees in agricultural-related disciplines like forestry, agricultural economics, etc."
Recently from the New York Times: (For Today’s Graduate, Just One Word: Statistics )
"Though at the fore, statisticians are only a small part of an army of experts using modern statistical techniques for data analysis. Computing and numerical skills, experts say, matter far more than degrees. So the new data sleuths come from backgrounds like economics, computer science and mathematics."
To quote, from Johns Hopkins University’s applied economics program home page:
“Economic analysis is no longer relegated to academicians and a small number of PhD-trained specialists. Instead, economics has become an increasingly ubiquitous as well as rapidly changing line of inquiry that requires people who are skilled in analyzing and interpreting economic data, and then using it to effect decisions ………Advances in computing and the greater availability of timely data through the Internet have created an arena which demands skilled statistical analysis, guided by economic reasoning and modeling.”
Finally, a quote I found on the (formerly) American Agricultural Economics Association's web page a few years ago:
“Nearly one in five jobs in the United States is in food and fiber production and distribution. Fewer than three percent of the people involved in the agricultural industries actually work on the farm. Graduates in agricultural and applied economics or agribusiness work in a variety of institutions applying their knowledge of economics and business skills related to food production, rural development and natural resources.”
"The combination of quantitative training and applied work makes agricultural economics graduates an extremely well-prepared source of employees for private industry. That's why American Express has hired over 80 agricultural economists since 1990." - David Edwards, Vice President-International Risk Management, American Express
Applied Economics is a broad field covering many topics beyond those stereotypically thought of as pertaining to agriculture. These may include finance and risk management, environmental and natural resource economics, behavioral economics, game theory, or public policy analysis to name a few. More and more 'Agricultural Economics' is becoming synonymous with 'Applied Economics.' Many departments have changed their name from Agricultural Economics to Agricultural and Applied Economics and some have even changed their degree program names to just 'Applied Economics.' In 2008, the American Agricultural Economics Association changed its name to the Agricultural and Applied Economics Association.
This trend is noted in recent research in the journal Applied Economic Perspectives and Policy:
"Increased work in areas such as agribusiness, rural development, and environmental economics is making it more difficult to maintain one umbrella organization or to use the title “agricultural economist” ... the number of departments named" Agricultural Economics” has fallen from 36 in 1956 to 9 in 2007."
Agricultural/Applied economics provides students with skills in high demand, particularly in the area of analytics.
"Some companies have built their very business on their ability to collect, analyze, and act on data." (See 'Competing on Analytics." Harvard Bus.Review Jan 2006)
In a recent blog post, SAS (a leader in applied analytics, big data, and software solutions) highlights the fact that they find people with applied economics backgrounds among their exectives:
"computer science may not be the best place to find data scientists....Over the years many of our senior executives have had degrees in agricultural-related disciplines like forestry, agricultural economics, etc."
Recently from the New York Times: (For Today’s Graduate, Just One Word: Statistics )
"Though at the fore, statisticians are only a small part of an army of experts using modern statistical techniques for data analysis. Computing and numerical skills, experts say, matter far more than degrees. So the new data sleuths come from backgrounds like economics, computer science and mathematics."
To quote, from Johns Hopkins University’s applied economics program home page:
“Economic analysis is no longer relegated to academicians and a small number of PhD-trained specialists. Instead, economics has become an increasingly ubiquitous as well as rapidly changing line of inquiry that requires people who are skilled in analyzing and interpreting economic data, and then using it to effect decisions ………Advances in computing and the greater availability of timely data through the Internet have created an arena which demands skilled statistical analysis, guided by economic reasoning and modeling.”
Finally, a quote I found on the (formerly) American Agricultural Economics Association's web page a few years ago:
“Nearly one in five jobs in the United States is in food and fiber production and distribution. Fewer than three percent of the people involved in the agricultural industries actually work on the farm. Graduates in agricultural and applied economics or agribusiness work in a variety of institutions applying their knowledge of economics and business skills related to food production, rural development and natural resources.”
UPDATE: This brief podcast from the University of Minnesota's Department of Applied Economics does a great job covering the breadth of questions and problems applied economists address in their work
https://podcasts.apple.com/mt/podcast/what-is-applied-economics/id419408183?i=1000411492398
UPDATE: See also Economists as Data Scientists http://econometricsense.blogspot.com/2012/10/economists-as-data-scientists.html
References:
'What is the Future of Agricultural Economics Departments and the Agricultural and Applied Economics Association?' By Gregory M. Perry. Applied Economic Perspectives and Policy (2010) volume 32, number 1, pp. 117–134.
'Competing on Analytics.' Harvard Bus.Review Jan 2006
‘For Today’s Graduate, Just One Word: Statistics.’ Steve Lohr. August 5, 2009
UPDATE: See also Economists as Data Scientists http://econometricsense.blogspot.com/2012/10/economists-as-data-scientists.html
References:
'What is the Future of Agricultural Economics Departments and the Agricultural and Applied Economics Association?' By Gregory M. Perry. Applied Economic Perspectives and Policy (2010) volume 32, number 1, pp. 117–134.
'Competing on Analytics.' Harvard Bus.Review Jan 2006
‘For Today’s Graduate, Just One Word: Statistics.’ Steve Lohr. August 5, 2009
Decision Trees
DECISION TREES: 'Classification and Decision Trees'(CART) Divides the training set into rectangles (partitions) based on simple rules and a measure of 'impurity.' (recursive partitioning) Rules and partitions can be visualized as a 'tree.' These rules can then be used to classify new data sets.
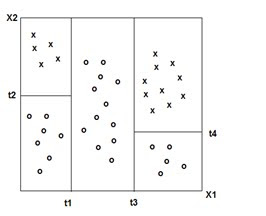
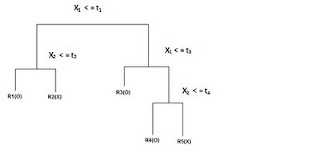
(Adapted from ‘The Elements of Statistical Learning ‘ Hasti, Tibshirani,Friedman)
RANDOM FORESTS: An ensemble of decision trees.
CHI-SQUARED AUTOMATIC INTERACTION DETECTION: characterized by the use of a chi-square test to stop decision tree splits. (CHAID) Requires more computational power than CART.


(Adapted from ‘The Elements of Statistical Learning ‘ Hasti, Tibshirani,Friedman)
RANDOM FORESTS: An ensemble of decision trees.
CHI-SQUARED AUTOMATIC INTERACTION DETECTION: characterized by the use of a chi-square test to stop decision tree splits. (CHAID) Requires more computational power than CART.
Neural Networks
NEURAL NETWORK: A nonlinear model of complex relationships composed of multiple 'hidden' layers (similar to composite functions)
Y = f(g(h(x)) or
x -> hidden layers ->Y
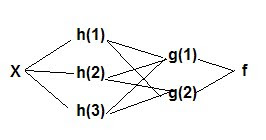
Example 1 With a logistic/sigmoidal activation function, a neural network can be visualized as a sum of weighted logits:
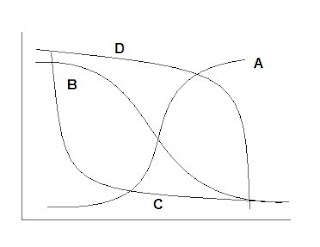
Y = α Σ wi e θi/1 + e θi + ε
wi = weights θ = linear function Xβ
Y= 2 + w1 Logit A + w2 Logit B + w3 Logit C + w4 Logit D
( Adapted from ‘A Guide to Econometrics, Kennedy, 2003)
Example 2
Y = f(g(h(x)) or
x -> hidden layers ->Y

Example 1 With a logistic/sigmoidal activation function, a neural network can be visualized as a sum of weighted logits:

Y = α Σ wi e θi/1 + e θi + ε
wi = weights θ = linear function Xβ
Y= 2 + w1 Logit A + w2 Logit B + w3 Logit C + w4 Logit D
( Adapted from ‘A Guide to Econometrics, Kennedy, 2003)
Example 2
Where: Y= W0 + W1 Logit H1 + W2 Logit H2 + W3 Logit H3 + W4 Logit H4 and
H1= logit(w10 +w11 x1 + w12 x2 )
H2 = logit(w20 +w21 x1 + w22 x2 )
H3 = logit(w30 +w31 x1 + w32 x2 )
The links between each layer in the diagram correspond to the weights (w’s) in each equation. The weights can be estimated via back propagation.
( Adapted from ‘A Guide to Econometrics, Kennedy, 2003 and Applied Analytics Using SAS Enterprise Miner 6.1)
MULTILAYER PERCEPTRON: a neural network architecture that has one or more hidden layers, specifically having linear combination functions in the hidden and output layers, and sigmoidal activation functions in the hidden layers. (note: a basic logistic regression function can be visualized as a single layer perceptron)
RADIAL BASIS FUNCTION (architecture): a neural network architecture with exponential or softmax (generalized multinomial logistic) activation functions and radial basis combination functions in the hidden layers and linear combination functions in the output layers.
RADIAL BASIS FUNCTION: A combination function that is based on the Euclidean distance between inputs and weights
ACTIVATION FUNCTION: formula used for transforming values from inputs and the outputs in a neural network.
COMBINATION FUNCTION: formula used for combining transformed values from activation functions in neural networks.
HIDDEN LAYER: The layer between input and output layers in a neural network.
HIDDEN LAYER: The layer between input and output layers in a neural network.
Data Mining in A Nutshell
# The following code may look rough, but simply paste into R or
# a text editor (especially Notepad++) and it will look
# much better.
# PROGRAM NAME: MACHINE_LEARNING_R
# DATE: 4/19/2010
# AUTHOR : MATT BOGARD
# PURPOSE: BASIC EXAMPLES OF MACHINE LEARNING IMPLEMENTATIONS IN R
# DATA USED: GENERATED VIA SIMULATION IN PROGRAM
# COMMENTS: CODE ADAPTED FROM : Joshua Reich (josh@i2pi.com) April 2, 2009
# SUPPORT VECTOR MACHINE CODE ALSO BASED ON :
# ëSupport Vector Machines in Rî Journal of Statistical Software April 2006 Vol 15 Issue 9
#
# CONTENTS: SUPPORT VECTOR MACHINES
# DECISION TREES
# NEURAL NETWORK
# load packages
library(rpart)
library(MASS)
library(class)
library(e1071)
# get data
# A simple function for producing n random samples
# from a multivariate normal distribution with mean mu
# and covariance matrix sigma
rmulnorm <- function (n, mu, sigma) {
M <- t(chol(sigma))
d <- nrow(sigma)
Z <- matrix(rnorm(d*n),d,n)
t(M %*% Z + mu)
}
# Produce a confusion matrix
# there is a potential bug in here if columns are tied for ordering
cm <- function (actual, predicted)
{
t<-table(predicted,actual)
t[apply(t,2,function(c) order(-c)[1]),]
}
# Total number of observations
N <- 1000 * 3# Number of training observations
Ntrain <- N * 0.7 # The data that we will be using for the demonstration consists
# of a mixture of 3 multivariate normal distributions. The goal
# is to come up with a classification system that can tell us,
# given a pair of coordinates, from which distribution the data
# arises.
A <- rmulnorm (N/3, c(1,1), matrix(c(4,-6,-6,18), 2,2))
B <- rmulnorm (N/3, c(8,1), matrix(c(1,0,0,1), 2,2))
C <- rmulnorm (N/3, c(3,8), matrix(c(4,0.5,0.5,2), 2,2))
data <- data.frame(rbind (A,B,C))
colnames(data) <- c('x', 'y')
data$class <- c(rep('A', N/3), rep('B', N/3), rep('C', N/3))
# Lets have a look
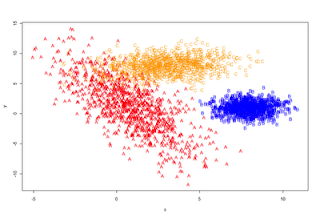
plot_it <- function () {plot (data[,1:2], type='n')
points(A, pch='A', col='red')
points(B, pch='B', col='blue')
points(C, pch='C', col='orange')
}
plot_it()
# Randomly arrange the data and divide it into a training
# and test set.
data <- data[sample(1:N),]train <- data[1:Ntrain,]
test <- data[(Ntrain+1):N,]
# SVM
# Support vector machines take the next step from LDA/QDA. However
# instead of making linear voronoi boundaries between the cluster
# means, we concern ourselves primarily with the points on the
# boundaries between the clusters. These boundary points define
# the 'support vector'. Between two completely separable clusters
# there are two support vectors and a margin of empty space
# between them. The SVM optimization technique seeks to maximize
# the margin by choosing a hyperplane between the support vectors
# of the opposing clusters. For non-separable clusters, a slack
# constraint is added to allow for a small number of points to
# lie inside the margin space. The Cost parameter defines how
# to choose the optimal classifier given the presence of points
# inside the margin. Using the kernel trick (see Mercer's theorem)
# we can get around the requirement for linear separation
# by representing the mapping from the linear feature space to
# some other non-linear space that maximizes separation. Normally
# a kernel would be used to define this mapping, but with the
# kernel trick, we can represent this kernel as a dot product.
# In the end, we don't even have to define the transform between
# spaces, only the dot product distance metric. This leaves
# this algorithm much the same, but with the addition of
# parameters that define this metric. The default kernel used
# is a radial kernel, similar to the kernel defined in my
# kernel method example. The addition is a term, gamma, to
# add a regularization term to weight the importance of distance.
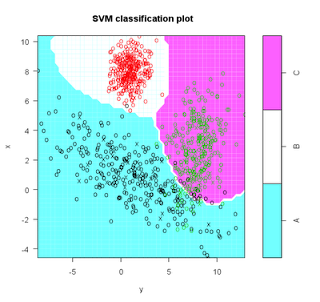
s <- svm( I(factor(class)) ~ x + y, data = train, cost = 100, gama = 1)
s # print model results
#plot model and classification-my code not originally part of this
plot(s,test)
(m <- cm(train$class, predict(s)))
1 - sum(diag(m)) / sum(m)
(m <- cm(test$class, predict(s, test[,1:2])))
1 - sum(diag(m)) / sum(m)
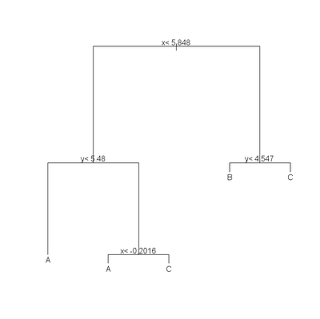
# Recursive Partitioning / Regression Trees
# rpart() implements an algorithm that attempts to recursively split
# the data such that each split best partitions the space according
# to the classification. In a simple one-dimensional case with binary
# classification, the first split will occur at the point on the line
# where there is the biggest difference between the proportion of
# cases on either side of that point. The algorithm continues to
# split the space until a stopping condition is reached. Once the
# tree of splits is produced it can be pruned using regularization
# parameters that seek to ameliorate overfitting.
names(train)names(test)
(r <- rpart(class ~ x + y, data = train)) plot(r) text(r) summary(r) plotcp(r) printcp(r) rsq.rpart(r)
cat("\nTEST DATA Error Matrix - Counts\n\n")
print(table(predict(r, test, type="class"),test$class, dnn=c("Predicted", "Actual")))
# Here we look at the confusion matrix and overall error rate from applying
# the tree rules to the training data.
predicted <- as.numeric(apply(predict(r), 1, function(r) order(-r)[1]))
(m <- cm (train$class, predicted))
1 - sum(diag(m)) / sum(m)
# Neural Network
# Recall from the heuristic on data mining and machine learning , a neural network is # a nonlinear model of complex relationships composed of multiple 'hidden' layers
# (similar to composite functions)
# Build the NNet model.
require(nnet, quietly=TRUE)
crs_nnet <- nnet(as.factor(class) ~ ., data=train, size=10, skip=TRUE, trace=FALSE, maxit=1000)
# Print the results of the modelling.
print(crs_nnet)
print("
Network Weights:
")
print(summary(crs_nnet))
# Evaluate Model Performance
# Generate an Error Matrix for the Neural Net model.
# Obtain the response from the Neural Net model.
crs_pr <- predict(crs_nnet, train, type="class")
# Now generate the error matrix.
table(crs_pr, train$class, dnn=c("Predicted", "Actual"))
# Generate error matrix showing percentages.
round(100*table(crs_pr, train$class, dnn=c("Predicted", "Actual"))/length(crs_pr))
Calucate overall error percentage.
print( "Overall Error Rate")
(function(x){ if (nrow(x) == 2) cat((x[1,2]+x[2,1])/sum(x)) else cat(1-(x[1,rownames(x)])/sum(x))}) (table(crs_pr, train$class, dnn=c("Predicted", "Actual")))
Subscribe to:
Posts (Atom)



