I found the following from Denver SAS Users Group presentation (link):

I use SAS in our advanced undergraduate statistics courses.

The advantages of using SAS over the common spreadsheet-based statistical packages,

such as Minitab or SPSS, are:

1.  The students are exposed to the logic of data management and data manipulations.

2.  It involves creative programming, while other packages are mostly menu driven.

3.  The wide scope of statistical capabilities enables us to work with more elaborate

     settings.

4.  Knowledge of SAS gives an advantage in the job market.

Yet, it is not too difficult for students to learn it  (At the basic level).

 I would agree, and this would just as easily apply to R as to SAS on all counts above. Most important, I think, is how spreadsheets and menu-driven packages overlook #1, which is just as important, I repeat just as important as the actual analysis. In the age of data science, not being equipped to manage and manipulate data (hacking skills) can leave you high and dry. Who cares if you can run a regression, the IT department probably isn't going to have time to get you the data exactly as you need it, and it might take several iterations of requests to get just what you need. And, without hacking skills, you may not even have the ability to recognize the fact that the data you have is not in fact the data you think it is.  And who says IT will always be able to hand you the data you want. Learning statistics with the an attitude that just assumes the data will be there and moves on with theory and analysis is OK as long as you take another course that follows that includes hacking/coding/data management. And guess what, that's not going to be done easily without some scripting language vs. pointing and clicking. This mindset I'll master stats and the data will just come on its own, might make a great statistician, but a poor data scientist.

 The importance of  these skills are illustrated very clearly in a recent Radar O'Reilly piece Building Data Science Teams.

"Most of the data was available online, but due to its size, the data was in special formats and spread out over many different systems. To make that data useful for my research, I created a system that took over every computer in the department from 1 AM to 8 AM. During that time, it acquired, cleaned, and processed that data. Once done, my final dataset could easily fit in a single computer's RAM. And that's the whole point. The heavy lifting was required before I could start my research. Good data scientists understand, in a deep way, that the heavy lifting of cleanup and preparation isn't something that gets in the way of solving the problem: it is the problem."

 I think that last statement says it all.

 And, besides valuable jobs skills, learning to code offers students a sense of empowerment. As quoted from a recent piece in Slate (HT Stephen Turner @ Getting Genetics Done):

“Learning to code demystifies tech in a way that empowers and enlightens. When you start coding you realize that every digital tool you have ever used involved lines of code just like the ones you're writing, and that if you want to make an existing app better, you can do just that with the same foreach and if-then statements every coder has ever used.”

This has been kind of a rant. I'm not sure what the solution is. I'm not sure how much of this can actually be taught in the classroom, and the time constraints can be binding.  I'm not sure data management and statistical analysis both need to be part of the same course.  I learned a lot of both on the job, and still have much to learn from a coding perspective. But I think at least making the effort to acquaint yourself with a language that is used industry wide (like SAS or R, or even  SPSS if the scripting language is introduced) as opposed to just any point and click interface with little data management capability seems to me to at least be a start.

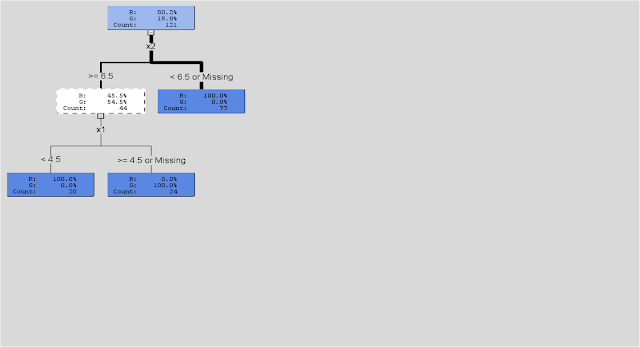
Decision Tree Basics in SAS and R

Assume we were going to use a decision tree to predict ‘green’ vs. ‘’red” cases (see below- note this plot of the data was actually created in R).

 

We want to use 2 variables say X₁ and X₂ to make a prediction of ‘green’ or ‘red’.  In its simplest form, the decision tree algorithm searches through the values of X₁ and X₂ and finds the values that do the ‘best’ job of ‘splitting’ the cases. For each possible value of X, the algorithm performs a chi-square test. The values that create the best ‘split’ (in SAS Enterprise Miner this is based on a metric called ‘worth’ which is a function of the p-value  associated with the chi-square test  [worth = -log(p-value)]) are chosen. (See below)

 

After all of the ‘best’ splits are determined, these values then become rules for distinguishing between cases (in this case ‘green’ vs. ‘red’) What you end up with in the end is a set of ‘rectangles’ defined by a set of ‘rules’ that can be visualized by a ‘tree’ diagram (see visualization from R below). 

 

 (see visualization from SAS Enterpise Miner Below)

But, in SAS Enterprise Miner, the algorithm then goes on to look at new data (validation data) and assesses how well the splitting rules do in terms of predicting or classifying new cases.  If it finds that a ‘smaller’ tree with fewer  variables or fewer splits or rules or ‘branches’ does a better job, it prunes or trims the tree and removes them from the analysis.  In the end, you get a final set of rules that can then be applied algorithmically to predict new cases based on observed values of X₁ and  X₂ (or whatever variables are used by the tree).

In SAS Enterprise Miner, with each split created by the decision tree, a metric for importance based on the Gini impurity index (which is a measure of variability or impurity for categorical data) is calculated. This measures how well the tree distinguishes between cases (again ‘green’ vs. ‘red’ or ‘retained’ vs. ‘non-retained’ in our model) and ultimately how well the model explains whatever it is we are trying to predict.  Overall, if splits based on values of X₂ ‘reduce impurity’ more so than splits based on values of  X₁ , then  X₂ would be considered the ‘best’ or ‘most’ predictive variable. 

The rpart algorithm used in R may differ in some of the specific details, but as discussed in The Elements of Statistical Learning (Hastie, Tibshirani and Friedman (2008)) all decision trees pretty much work the same, fitting the model by recursively partitioning the feature space into rectangular subsets.

 R code for the Decision Tree and Visualizations Above: 

# *------------------------------------------------------------------
# | PROGRAM NAME: R_tree_basic 
# | DATE:4/26/11    
# | CREATED BY: Matt Bogard 
# | PROJECT FILE:P:\R  Code References\Data Mining_R              
# *----------------------------------------------------------------
# | PURPOSE: demo of basic decision tree mechanics               
# |
# *------------------------------------------------------------------
 
rm(list=ls()) # get rid of any existing data 
ls() # view open data sets
 
setwd('/Users/wkuuser/Desktop/R Data Sets') # mac 
setwd("P:\\R  Code References\\R Data") # windows
 
library(rpart) # install rpart decision tree library
 
# *------------------------------------------------------------------
# | get data            
# *-----------------------------------------------------------------
 
dat1 <-  read.csv("basicTree.csv", na.strings=c(".", "NA", "", "?"), encoding="UTF-8")
plot( dat1$x2, dat1$x1, col = dat1$class) # plot data space
 
# fit decision tree
 
(r <- rpart(class ~ x1 + x2, data = dat1)) 
 
plot(r)
text(r)
 
library(rattle) # data mining package
drawTreeNodes(r) # for more detailed tree plot supported by rattle

Created by Pretty R at inside-R.org

Predictive Analytics In Higher Ed

See also: Using SAS® Enterprise BI and SAS® Enterprise Miner™ to

Reduce Student Attrition & A Mandate For Causal Inference in Higher Education

A colleague shared with me the following article The Predictive Analytics Reporting Framework Moves Forward . This is a great example of the 'multicultural' approach to data analysis that I had discussed in 'Culture War: Classical Statistics vs. Machine Learning'

From the article:

Wagner: "For some in education what we’re doing might seem a bit heretical at first--we’ve all been warned in research methods classes that data snooping is bad! But the newer technologies and the sophisticated analyses that those technologies have enabled have helped us to move away from looking askance at pattern recognition. That may take a while in some research circles, but in decision-making circles it’s clear that pattern recognition techniques are making a real difference in terms of the ways numerous enterprises in many industries are approaching their work"

The fact that they are willing to step out of what Leo Brieman described as the 'statistical straight jacket' of traditional research methods and embrace 'heretical' pattern recognition and data mining algorithms is impressive. The paragraph excerpted above and the distinction between 'research circles' and 'decision making circles' indicates to me they clearly get what he was talking about over a decade ago in his famous article 'Two Statistical Cultures' ( http://bit.ly/bqtZ6I ).

"There are two cultures in the use of statistical modeling to reach conclusions from data. One assumes that the data are generated by a given stochastic data model. The other uses algorithmic models and treats the data mechanism as unknown. The statistical community has been committed to the almost exclusive use of data models. (i.e. 'research circles') This commitment has led to irrelevant theory, questionable conclusions, and has kept statisticians from working on a large range of interesting current problems.Algorithmic modeling,both in theory and practice,has developed rapidly in fields outside statistics."(like 'decision making circles').

As far as 'newer' technologies and the 'sophisticated analysis' that they can employ, I can only see opportunities for programs like SAS Enterprise Miner, JMP, and R.

Reference:
Leo Breiman. Statistical Modeling: The Two Cultures.  Statist. Sci. Volume 16, Issue 3 (2001), 199-231.

Time Series Intervention Analysis with R and SAS

In a previous post, I worked through the theory behind intervention analysis. In his time series course, University of Georgia political science professor Jamie Monogan demonstrates how to implement intervention analysis in R.  The following example is from this course. It investigates the impact of the terrorist attacks of 911 on president Bush's approval ratings. An excerpt from the data set follows:


   year month  approve  t s11
1  2001     1 45.41947  1   0
2  2001     2 55.83721  2   0
3  2001     3 55.91828  3   0
4  2001     4 58.12725  4   0
5  2001     5 55.79231  5   0
.
.
.
etc

Note in the plot of the series above, observation 10 represents October 2001, post 9/11/2011. It appears that there is a drastic shift in the series, that slowly decays and eventually returns to previous levels. This may indicate an intervention model with a pulse function.  Following the Box-Jenkins methodology, an ARIMA(1,0,0) model with the intervention can be specified in R as follows:

model <- arimax(bush$approve, order=c(1,0,0), xtransf=bush$s11, transfer=list(c(1,0)))

where:
bush$approve = Yt , Bush's approval ratings
order =c(1,0,0) indicates and AR(1) process
xtransf=bush#s11 is the intervention series, flagging Pt = 1 to indicate September 11, 2001
transfer = list(c(1,0))  indicates the functional form of the transfer function. The first parameter indicates the denominator, while the second indicates a numerator factor. As specified in the code above the transfer function is specified as follows:

[w0/ 1- δB ]

Based on SAS documentation (http://support.sas.com/documentation/cdl/en/etsug/60372/HTML/default/viewer.htm#etsug_arima_sect014.htm )  this could also be specified in SAS via PROC ARIMA as follows:

   proc arima data=bush;
      identify var=approve crosscorr=s11;
      estimate p =1  input=( / (1) s11 );
   run;

Using R, the estimated model coefficients are:
Coefficients:
         ar1  intercept  T1-AR1   T1-MA0
      0.8198    58.2875  0.8915  23.6921
s.e.  0.1184     4.6496  0.0166   3.9415

Based on the output above, w0 = 23.6921 and δ = .8915. The plot below shows the fitted values which look very similar the to graphs for this specification shown in the previous post.

The code below is was used to conduct this analysis, and is excerpted from Jamie Monogan's original R program.

#   ------------------------------------------------------------------
#  | PROGRAM NAME: R_ARIMAX
#  | DATE:1/21/12
#  | CREATED BY: Matt Bogard 
#  | PROJECT FILE: /Users/wkuuser/Desktop/Briefcase/R Programs              
#  |----------------------------------------------------------------
#  | PURPOSE: illustration of ARIMA model with transfer function/intervention series               
#  |
#  |
#  | 
#  |------------------------------------------------------------------
#  | COMMENTS: R code and data originally sourced from : http://monogan.myweb.uga.edu/teaching/ts/index.html
#  |------------------------------------------------------------------
 
#libraries
rm(list=ls())
library(foreign)
library(TSA)
 
setwd('/Users/wkuuser/Desktop/briefcase/R Data Sets') # mac 
 
#load data & view series
 
bush <- read.dta("BUSHJOB.DTA")
names(bush)
print(bush)
 
plot(y=bush$approve, x=bush$t, type='l')
 
#identify arima process
acf(bush$approve)
pacf(bush$approve)
 
#estimate arima model
mod.1 <- arima(bush$approve, order=c(0,1,0))
mod.1
 
#diagnose arima model
acf(mod.1$residuals)
pacf(mod.1$residuals)
Box.test(mod.1$residuals)
 
#Looks like I(1). Note: There is a theoretical case against public opinion data being integrated.
 
#estimate intervention analysis for september 11 (remember to start with a pulse
 
mod.2 <- arimax(bush$approve, order=c(0,1,0), xtransf=bush$s11, transfer=list(c(1,0))); mod.2
 
summary(mod.2)
 
#Notes: the second parameter directs the numerator. If 0 only, then concurrent effect only. The first parameter affects the denominator. c(0,0) replicates the effect of just doing "xreg"
#Our parameter estimates look good, no need to drop delta or switch to a step function.
 
#Graph the intervention model
y.diff <- diff(bush$approve)
t.diff <- bush$t[-1]
y.pred <- 24.3741*bush$s11 + 24.3741*(.9639^(bush$t-9))*as.numeric(bush$t>9)
y.pred <- y.pred[-1]
plot(y=y.diff, x=t.diff, type='l')
lines(y=y.pred, x=t.diff, lty=2)
 
#suppose an AR(1) process
mod.2b <- arimax(bush$approve, order=c(1,0,0), xtransf=bush$s11, transfer=list(c(1,0))); mod.2b
y.pred <- 58.2875 + 23.6921*bush$s11 + 23.2921*(.8915^(bush$t-9))*as.numeric(bush$t>9)
plot(y=bush$approve, x=bush$t, type='l')
lines(y=y.pred, x=bush$t, lty=2)

Created by Pretty R at inside-R.org

Intervention Analysis

See also: Time Series Intervention Analysis with R and SAS

In previous posts I have discussed the basics of time series analysis methods, provided an example of an applied ARIMA model (using fertilizer application data), and discussed how vector auto regressions can be used to accommodate a multivariate analysis of time series. What if you want to measure the impact of some shock or event (such as a change in government policy, the impact of a natural disaster, a negative news report etc. ) on a the behavior of a series of data?  For instance, lets assume beef consumption was holding steady or even trending downward. Then at time ‘t’ someone of national prominence or importance makes false claims about beef safety. We notice a downward trend in beef consumption follows.  How much of this decrease can be attributed to the headline making false claims, and how much is just the continued momentum of other factors.  Or, assume that corn prices have been trending upward for some time and at some time ‘t’, the government increases renewable fuels mandates. It follows that we notice an increase in the trend of corn prices. How much of this can be attributed to the public policy vs. the momentum of other evolving factors? 

Time series intervention analysis (ARIMA modeling with intervention) provides the framework for answering these types of questions.  As explained in the introductory business forecasting text written by Newbold and Bos:

“ When a significant intervention has interrupted the stable behavior of a time series of interest, it is important to attempt to explicitly model its impact. Box and Tao(1975) introduced a procedure , known as intervention analysis, for this purpose. Essentially these authors proposed the use of the transfer function-noise class of models…but with Xt a dummy variable series defined to take the value zero up to the point in time that the intervention occurs, and the value one thereafter.”

As described by Nelson (2000) intervention analysis is

“an extension of the ARIMA methods introduced by Box and Tao (1975) and Jenkins(1976) to measure the effect of a policy change or event on the outcome of a variable...In summary, intervention models generalize the univariate Box-Jenkins methodology by allowing the time path of the dependent variable to be influenced by the time path of the intervention variables”

So it seems a time series intervention analysis can be a valuable tool for assessing the impact of some policy change or other intervention on the trend of some variable we are interested in. This however first requires an understanding of the transfer function-noise class of models described by Newbold and Bos.

Transfer Functions

ARIMA models are simply models of a single dependent variable  (Y) as a function of past values of Y as well as past values of the error terms (e).

For example, ARIMA(2,1,1) :    Y*_t = b₀ + b₁Y*_t-1  + b₂Y*_t-2  + b₃ e_t-1  + e_t  represents an ARIMA model with 2 autoregressive terms, 1 first difference, and 1 moving average term.  But what if we want to include the impact of some other variable on Y, such as X.  A basic regression model Y = B0 + B1X provides a static model for this relationship, but what if we want a model that captures this relationship between both the time path of X and Y.  One way to look at the impact of the time path of X on Y would be to model:

Yt = V0 + V1Xt + V2Xt-1 + V3Xt-3 +…..et

 

This can more compactly, flexibly, and efficiently be represented and estimate as

Yt = α +w(B)/ δ(B) *Xt + e_t 

where:

w(B) = wo + w1B +w2B +…wrB^r

δ(B) = 1- δ1B -… -δ_s B^s

B = the backshift operator

Xt  = the independent explanatory variable of interest

e_t  =noise/error term

As pointed out by Newbold and Bos, this model often can fit many data series quite well with only a few polynomial terms, such as the very popular formulation below:

Yt = α +[wo/ 1- δ1B ]*Xt + e_t 

Which is equivalent to:

Yt = α + woXt + wo δ1Xt-1 + woδ₁² Xt-2 + woδ₁³ Xt-3 +…+ e_t 

This model implies that a 1 unit increase in X during time t increases Y by wo units, increases Y by wo δ1 units in the next time period  and by woδ₁² units the following period with the impact of the change in X phasing out over time.  The polynomial expression [wo/ 1- δ1B ]*Xt represents what’s referred to as a transfer function.

What about the time path of Y itself? We previously modeled this via an ARIMA process. Letting e_t  be represented by the ARIMA process ( aka noise process Nt) as follows:

[θ(B) θ(B^s) / Φ(B) Φ(B^s) Δ^dΔ^s  ] *   a_t   where  

B = backshift operator such that BY = Yt-1

θ(B) = MA(q)

θ(B^s) = seasonal MA(Q)

Φ(B) = AR(p)

Φ(B^s) = seasonal AR(P)

Δ^d=  differencing

Δ^s = seasonal differencing

a_t = white noise term

which is just another way of representing the ARIMA(p,d,q)(P,D,Q) process where

P = # of seasonally differenced autoregressive terms
D = # of seasonal differences
Q = # of seasonally differenced moving average terms

The combined transfer function-noise model can be represented more compactly as:

Yt = C + w(B)/ δ(B) *Xt + Nt

Or even more compactly:

Yt = C + v(B)*Xt + Nt

This brings us back to the description of intervention analysis previously described by Bos and Newbold:

Essentially these authors proposed the use of the transfer function-noise class of models…but with Xt a dummy variable series defined to take the value zero up to the point in time that the intervention occurs, and the value one thereafter.”

That is, we use the noise-transfer model above, with the independent variable Xt being a dummy or indicator variable flagging the intervention at time ‘T’.  If we let Xt  be the intervention variable I_t, it can take two forms, depending on they impact of the intervention on the series of interest (Y):

Let I_t be a pulse function St such that:

Pt =  0 if  t != T

           1 if t = T

Pulse functions are typically employed if the effects are  expected to be only temporary, and decay over time.

Let I_t be a step function St such that:

St = 0 if t < T

       1 if t >= T

Step functions are typically employed if the effects of the intervention are expected to remain permanently after time T.

So a time series intervention model can be compactly expressed in two ways, as a pulse function:

Yt = C + v(B)*Pt + Nt

Or as a step function

Yt = C + v(B)*St + Nt

 Min(2008) provides some interesting graphs illustrating these various specifications.

Pulse: [wB/ 1- δB ]Pt

 

The above specification illustrates an intervention with an abrupt temporary effect ‘w’ that gradually decay or ‘wears off’ at rate δ with a return back to original or pre-intervention levels.

 Step: [wB/ 1- δB ]St

The above specification illustrates an intervention with a gradual permanent effect with an initial impact or level change of ‘w’ and rate of adjustment equal to δ and long run response level w/1- δB.  To better illustrate the role of δ, note that if δ = 0 then we would have [wB ]St. There would be no adjustment process as illustrated below.

 

There are many other possible specifications depending on the behavior of the series we are interested in (Yt) and the impact of the intervention on the time path of Yt.  As noted in Wei(1990) you can even specify a combination of step and pulse functions as follows:

[woB/ 1- δB ]Pt + w1St

It also follows that we could have both an input series Xt  (as discussed previously in the context of transfer functions) and an intervention It specified as follows:

Yt = C + v(B)*It + w1BXt + Nt

Where It is either a step or pulse function.

References:

 Consumer Bankruptcies and the Bankruptcy Reform Act: A Time-Series Intervention Analysis, 1960–1997. Jon P. Nelson. Journal of Financial Services Research

Volume 17, Number 2,  Aug 2000. 181-200, DOI: 10.1023/A:1008166614928

Box, G. E. P. and G. C. Tiao. 1975. “Intervention Analysis with
Applications to Economic and Environmental Problems.” Journal of the American Statistical Association. 70:70-79

Introductory Business Forecasting. Newbold and Bos. 1990.

Jennifer C.H. Min, (2008) "Forecasting Japanese tourism demand in Taiwan using an intervention analysis", International Journal of Culture, Tourism and Hospitality Research, Vol. 2 Iss: 3, pp.197 – 216

Time Series Analysis: Univariate and Multivariate Methods. William W.S.Wei. 1990.

Culture War (original post)

 'Statistical Modeling: The Two Cultures' by L. Breiman (Statistical Science

2001, Vol. 16, No. 3, 199–231) is an interesting paper that is a must read for anyone traditionally trained in statistics, but new to the concept of machine learning. It gives  perspective and context to anyone that may attempt to learn to use data mining software such as  SAS Enterprise Miner or who may take a course in machine learning  (like Dr. Ng's (Stanford) youtube lectures in machine learning .) The algorithmic machine learning paradigm is in great contrast to the traditional probabilistic approaches of 'data modeling' in which I had been groomed both as an undergraduate and in graduate school.

From the article, two cultures are defined:

"There are two cultures in the use of statistical modeling to reach conclusions from data.

Classical Statistics/Stochastc Data Modeling Paradigm:

" assumes that the data are generated by a given stochastic data model. "

Algorithmic or Machine Learning Paradigm:

"uses algorithmic models and treats the data mechanism as unknown."

In a lecture  for Eco 5385
 Data Mining Techniques for Economists
, Professor  Tom Fomby
 of Southern Methodist University distinguishes machine learning from classical statistical techniques:

Classical Statistics: Focus is on hypothesis testing of causes and effects and interpretability of models.  Model Choice is based on parameter significance and In-sample Goodness-of-fit.

Machine Learning:  Focus is on Predictive Accuracy even in the face of lack of interpretability of models.  Model Choice is based on Cross Validation of Predictive Accuracy using Partitioned Data Sets.

For some, this distinction may be made more transparent by comparing the methods used under each approach. Professor Fomby does a great job making these distinctions:

Methods Classical Statistics:  Regression, Logit/Probit, Duration Models, Principle Components, Discriminant Analysis, Bayes Rules

Artificial Intelligence/Machine Learning/Data Mining: Classification and Regression Trees, Neural Nets, K-Nearest Neighbors, Association Rules, Cluster Analysis

 

From the standpoint of econometrics, the data modeling culture is described very well in this post by Tim Harford:

"academic econometrics is rarely used for forecasting. Instead, econometricians set themselves the task of figuring out past relationships. Have charter schools improved educational standards? Did abortion liberalisation reduce crime? What has been the impact of immigration on wages?"

This is certainly consistent with the comparisons presented in the Statistical Science article. Note however, that the methodologies referenced in the article (like logistic regression)  that are utilized under the data modeling or classical statistics paradigm are a means to fill what Brieman refers to as a black box. Under this paradigm analysts are attempting to characterize an outcome by estimating parameters and making inferences about them based on some assumed data generating process. It is not to say that these methods are never used under the machine learning paradigm, but how they are used. The article provides a very balanced 'ping-pong' discussion citing various experts from both cultures, including some who seem to promote both including the authors of The Elements of Statistical Learning: Data Mining, Inference, and Prediction.

In my first econometrics course, the textbook cautioned against 'data mining,' described as using techniques such as stepwise regression. It insisted on letting theory drive model development, rating the model on total variance explained, and the significance of individual coefficients. This advice was certainly influenced by the 'data modeling' culture. The text was published in the same year as the Breiman article. ( I understand this caution has been moderated in contemporary editions).

Of course, as the article mentions, if what you are interested in is theory and the role of particular variables in underlying processes, then traditional inference seems to be the appropriate direction to take. (Breiman of course still takes issue, arguing that we can't trust the significance of an estimated co-efficient if the model overall is a poor predictor).

"Higher predictive accuracy is associated with more reliable information about the underlying data mechanism. Weak predictive accuracy can lead to questionable conclusions."

"Algorithmic models can give better predictive accuracy than data models,and provide better information about the underlying mechanism."

"The goal is not interpretability, but accurate information."

When algorithmic models are more appropriate (especially when the goal is prediction) a stoachastic model designed to make inferences about specific model co-efficients may provide "the right answer to the wrong question" as Emanuel Parzen puts it in his comments on Breiman.

While in graduate school, the stochastic culture was dominant. However, there was some inclusiveness, take for example Kennedy's A Guide to Econometrics . Kennedy discusses the expectation maximization algorithm (also a lecture in Dr. Ng's course) and also provides a great introduction to neural networks which greatly influenced my understanding of such allegedly 'uninterpretable' algorithmic techniques.

Keeping an Open Mind: Multiculturalism in Data Science

As  Breiman states:

"Approaching problems by looking for a data model imposes an apriori straight jacket that restricts the ability of statisticians to deal with a wide range of statistical problems."

A multicultural approach to analysis (stochastic or algorithmic) seems to be the take away message of the Breiman article and discussions that follow. In fact, this may be the best approach in the universe of all things empirical. This is certainly true in the new field of data science, and is clearly depicted in Drew Conway's  data science Venn diagram depicted below. 

As Parzen states "I believe statistics has many cultures." He points out that many practitioners are well aware of the divides that exist between Bayesians and frequentists, algorithmic approaches aside. Even if we restrict our tool box to stochastic methods, we can often find our hands tied if we are not open minded. We can still sacrifice results over technique. And there are plenty of divisive debates.  For example, in discussing the state of modern econometrics Leamer faults econometric results that emphasize statistical significance over practicality or importance in an interesting podcast from Econ Talk here.

Brieman touches on  his idea of importance as well:

"My definition of importance is based on prediction. A variable might be considered important if deleting it seriously affects prediction accuracy"

Note, no mention of statistical significance (a child of the stochastic data modeling culture) by  Breiman

This is echoed in a paper from the Joint Statistical Meetings-Section on Statistical Education (2009) 'The Cult of Statistical Significance' by Stephen T. Ziliak and Deirdre N. McCloskey who have authored a book by the same title.  They note:

"Statistical significance is, we argue, a diversion from the proper objects of scientific study…Significant does not mean important and insignificant does not mean unimportant"

I even find a hint of this in Greene, a well known econometrics textbook author:

 "It remains an interesting question for research whether fitting y well or obtaining good parameter estimates is a preferable estimation criterion. Evidently, they need not be the same thing."

  p. 686 Greene,  Econometric Analysis 5^th ed

It seems that cultural divides are hard to avoid. Take another example from the article below:

Statistical alternatives for studying college student retention: A comparative analysis of logit, probit, and linear regression. Eric L. Dey and Alexander W. Astin Research in Higher Education

Volume 34, Number 5, 569-581 (1993)

 The above article concluded:

"Results indicate that despite the theoretical advantages offered by logistic regression and probit analysis, there is little practical difference between either of these two techniques and more traditional linear regression. "

It never fails to go to a paper presentation and see someone getting uptight over linear probability models.  In fact, there is some interesting literature on the robustness and pragmatism of linear probability models. 

An emphasis on robustness  or even parsimony seems to be an overarching theme in the fairly new book "Mostly Harmless Econometrics" by Joshua Angrist and Jörn-Steffen Pischke. Angrist and Pishke write about  the robustness of the LPM in their book (but also see econometrician Dave Giles  post with some challenging objections to the LPM, a followup by Angrist and Pischke, and more discussion from economist Marc Bellemare).

Their web site for the book seems to caution practitioners about being married to fancier techniques:

fancier techniques are typically unnecessary and even dangerous.

I have become more and more open minded as my experience working under both paradigms has increased. Software packages like SAS Enterprise Miner certainly accommodate open minded curiosity. Packages like R  (or even SAS IML) let the very curious get their hands even dirtier. Both have been very influential to me. When it comes to estimating the marginal effects of a treatment for a binary outcome, I usually have no issue with using an LPM over logistic regression (but I would have taken issue with it not not long ago). But when it comes to prediction I certainly won't shy away from using logistic regression or for that matter a neural net, decision tree, or a 'multicultural' ensemble of all of the above.