Support Vector Machines

Separates classes utilizing supporting hyperplanes and a separating hyperplane that maximizes the margin between classes.



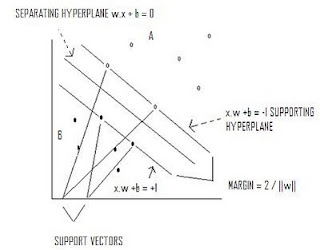
Max 2/||w|| s.t. y(x*w+b)-1 >=0

If data is not linearly separable, a kernel function can be used to map data into a space where it is linearly separable.

Input Space →Kernel Function →Feature Space →Input Space.

Quadratic programming provides a decision function:

D(x) = ∑ ∝ k(x_i,x_j) + b such that if D(x) >0 then x ∊ A

Kernel Functions

Mapping function x→φ(x)

linear kernel

k(x_i,x_j)=x_i'x_j

radial basis kernel

k(x_i,x_j) = exp[-(||x_i –x_j||^{2 / 2 σ2} )]

polynomial kernel

k(x_i,x_j) = (x_ix_j + a)b

sigmoidal kernel

k(x_i ,x_j) = tanh(x_ix_j - b)